В системе Ханкок расположена эскадра Хонор Харрингтон, капитана королевства Мантикоры.
wiki:Вселенная_Хонор_Харрингтон

В систему вторгся флот Народной Республики Хевен превосходящими силами.
Вероятность выстоять стремительно снижается с каждым днём по следующему графику: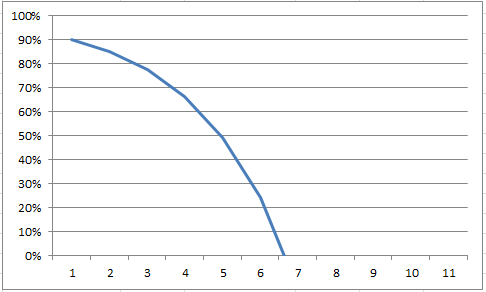


У Харрингтон есть 5 курьерских ботов с импеллерными двигателями, которые она может отправить на Мантикору через гиперпространство с просьбой о подкреплении.
Расстояние до Мантикоры — 100 световых лет.

Боты могут лететь на парусах Варшавской в разных полосах гравитационной волны с разной скоростью (значительно превышающей световую), но при этом вероятность долететь тоже резко уменьшается (см. таблицу ниже):

полоса - вероятность долететь - скорость	
1) альфа	- 100%		- 10 световых/день
2) бета 	- 95%		- 20 световых/день
3) гамма	- 80%		- 40 световых/день
4) дельта	- 70%		- 80 световых/день
5) эпсилон	- 50%		- 160 световых/день

Харрингтон надо выбрать, по какой полосе и сколько ботов отправить.
При этом Харрингтон знает, что на Мантикоре есть 3 свободные эскадры, каждая из которых может защитить Ханкок. Им тоже придётся выбирать, по какой полосе лететь от Мантикоры до Ханкока. После получения просьбы о помощи Королева может направить каждую эскадру по своей полосе.

Харрингтон не знает, что выберет Королева, но какое-то решение надо принять прямо сейчас, потому что систему надо защитить или отбить любой ценой, так как это стратегически важный пункт для всей Мантикоры.

Вопрос: по какой полосе и сколько курьерских ботов надо отправить, чтобы защитить/отбить Ханкок, пока хевениты её не захватили и не построили там свои космические верфи для нападения на Мантикору?

Надо понимать, эксперимент "на какой ветке народ перестанет реагировать на эту х.ню" закончен.
Огласите результат.

(1) Когда Ненавижу 1С создавал задачки-числодробилки (ниже примеры его веток), то вроде решали как-то. У меня каждая задача уникальна, с аутентичным игровым контекстом. Я подожду пару дней, может кто-то поймёт, что это задача на смекалку, а не на теорию вероятностей.

Примеры задачек от Ненавижу 1С

Семнадцать из трёх тысяч
Кубическое уравнение в целых положительных
Сумма четырех натуральных чисел делится на каждое из них

(1) Жестко и  иронично, но по делу.

(1) и собственно, почему Вы мне отказываете в праве придумывать методы удержания гуру и выявления новых гуру на моём собственном форуме? Может у Вас есть свой форум, где всё происходит по-другому?

Считайте это моим интеллектуальным хобби. Я же задачки придумываю через нейронки и проверяю решения тоже через них. Так что в моих ветках вы соревнуетесь с топовыми нейронками. Кто решил, тот и гуру.

(4) Никто тебе ни в чем не отказывает и не может отказать. Стас, твою ветку поддерживают как могут. Тебе бы благодарствовать за это, а ты в бутылку полез.

(6) Мои задачки набрали уже больше 1000 постов. Так что моя wiki:Бутылка_Клейна только открывается.

И вообще, должна же быть дежурная ветка для флуда среди гуру. Раньше была Хреноветка, потом завели Пятничные, теперь наш интеллектуальный уровень вырос, мы доросли до гуру

(0) Очевидно что все 5 ботов по 5-й полосе
Вероятность 0,99609375 очень неплоха
Сообщение будет доставлено за 0,625 дня

Вот с обратным маршрутом для 3-х эскадр все сильно хуже
Выбирать ниже 4-й полосы (0,973) опасно
Для вероятности 0,99 нужна 3-я полоса чтобы хотя бы один флот прибыл, а это 2,5 дня
К этому моменту вероятность выстоять уже ниже 80%

(9) 🔥 Расчёт — огонь! Но не 100%. Вы рискуете потерять звезду Ханкок и королевство в целом.

Задачи на смекалку не требуют вычисления вероятностей. Кто пошёл считать вероятности, тот проиграл.

Весь контекст задачи как бы призывает вас к вычислению вероятностей (суммированию и умножению), но разгадка чисто логическая. Вероятность можете вычислить постфактум, но решение на ладони.

(10) 100% невозможны поскольку мы стартуем уже на 90%

Раз задача на смекалку, то думаю раз у них есть возможность отправлять ботов на скоростях в десятки раз превышающих скорость света, то у них явно есть и телепорты. Следовательно можно сразу телепортировать всех ботов и победить с вероятностью 100%

Вероятность штука математическая и забавная.
В реале теория работает плохо.

Помню у Джека Лондона что то было.
Мужик выиграл по крупному в локальном казино.
Стол подсох. Шарик был не объективен.

Не смотря на то что вероятность выбросить "орел"
подкидывая монетку десять раз из десяти очень мала (многих обнадеживает в казино),
вероятность выпадения при каждом броске равна 50% (при честной игре).

Ну и как бы "не нужно полагаться на слепую удачу".
Бывают монеты с двумя орлами, на особый случай.

"по какой полосе и сколько курьерских ботов надо отправить"

ставите не решаемые задачи )))
с не точной постановкой. Правила игры точно знает только ТС.

Закон падающего бутерброда никто не отменял.

Туда летим всеми кораблями на максимальной скорости вероятность не долететь 3% тратим 0,625 дня.
Назад если всеми кораблями на максималке вероятность не долететь 12,5% прилетаем в 1,25 день вероятность проиграть 83%
Если на второй скорости то не долетим 2,7% по времени 1,88 дня
и вероятность проигрыша 85%
Вторая всеми точно выгоднее риск проигрыша изменяется на пару процентов, а долететь повышается в 4,6 раза

(18) Не прочитал (11)?

(13) Возможно

(19) Есть риск потери системы

(19) Вероятности криво посчитал, очень криво

Решение:
надо отправить 1 бота по полосе альфа, с вероятностью 100%. Остальных курьерских ботов надо отправить по самой быстрой эпсилон полосе для скорости.
Королева со своими эскадрами поступит так же: 1 эскадра по полосе альфа, 2 эскадры по полосе эпсилон.

Это даёт высокую вероятность защитить систему в первые 2 дня и даёт ГАРАНТИЮ отбить систему через 20 дней.

Эмм
Потерять 4 бота из 5-ти пофиг, но 2 эскадры из 3-х - так себе решение

Если пофиг на потери то достаточно отправить все 5 ботов по 3-й полосе гамма, там вероятность что хоть один долетит (причем быстро) 100%

В обратную сторону отправляем все 3 эскадры по 2-й полосе бета, аналогично хотя бы один долетит
Причем успеваем как раз к концу сражения, силы противника минимальны

(26) Да, но также есть и вероятность, что ни один не долетит.

(26) написано же: ЛЮБОЙ ЦЕНОЙ

(27) Летать на самолетах или ездить на машинах тоже опасно
Но летают и ездят
Тут вероятности лучше

(29) Кстати, самолет по статистике - самый безопасный вид транспорта. В отличие от машин :))

(0) или отбить любой ценой
Так как любая эскадра может победить, то с гарантией 100% отправляем бота по альфа и флот по альфа.
Цена высока, но гаратия 100%

(28) Уже 4 бота по 2-й полосе долетают 100% (вероятность 1)
5 ботов по 3-й с вероятностью 0,99999744

Аналогично 3 флота по 2-й полосе вероятность 0,999875 (это близко к 100%)

(30) А вот по статистике выживаемости он очень не очень.

(33) Ну тут тоже спорно, что лучше - гарантированно убиться в катастрофе сразу, или выжить и доживать потом парализованным овощем.

(32) близко, но не 100%

Имхо я бы на месте капитана отправил 4 бота по 2-й полосе и 1 бот по 5-й полосе
И приказал бы отступить после 3-го дня, если помощь не прилетит ранее

На месте королевы отправил бы 1-ю эскадру по 2-й полосе, 2-ю по 1-й полосе а 3-ю эскадру оставил в резерве

Вот только непонятно, как вероятность того, что бот долетит может зависеть от количества запущенных ботов?

Мне кажется, что тут, как с монеткой - сколько раз решка не выпадет, в следующий раз вероятность всё равно 50%.

Так и тут, мне кажется, вероятность долёта надо считать для каждого бота в отдельности.

(37) можно считать вероятности как зависимых так и независимых событий

(37) вероятность события, что долетит хотя бы один бот из четырёх, повышается по формуле 1-0.5⁴

(36) Да ты стратег! Чувствуется закалка, наработанная на стратегических играх

(25) Не дает. У наступающих должно быть 3-х кратное преимущество. Если 1 эскадры хватает чтобы защитить не факт что хватит на отбить.
В условие написано что 1 эскадры хватает чтобы именно "Защитить", а не "Победить"

(41) Про трёхкратное преимущество Вы уже придумали. Численность эскадр может быть различной, в задаче этой инфы нет.

(41) "В условие написано именно "Защитить" а не "Победить""
Где ты такое увидел?
В (0) написано: "систему надо защитить или отбить любой ценой,"

Согласен с (36) нужно одну эскадру в резерве держать. А то враг может на столицу напасть пока все 3 в отлете.

(44) Сказали же: есть 3 свободные эскадры. Наверняка есть занятые, которые охраняют саму Мантикору